【JavaScript＆HTML5講座】トップページへ

2-2 ゲーム制作の基礎知識２　ヒットチェック

ゲームで２つの物体が接触しているかを判定することをヒットチェック（あるいは接触判定や衝突判定）といいます。 アクションゲームなどでユーザーが操作するキャラと敵キャラが接触したかを調べるような処理が基本ですが、 例えばカードゲームで手持ちの札をタップ（マウスならドラッグドロップ）操作で魔方陣の上に置くゲームがあるなら、 カードと魔方陣の座標の位置関係の判定もヒットチェックと同様の手法で行うことができます。
フィールド（ＢＧ）上でキャラクターが入れる場所、入れない場所を調べることは当たり判定といい、 制作会社によってはキャラクターと背景のヒットチェックというところもあります。 当たり判定は別途解説します。
ヒットチェックがシビアに行われるアクションゲームは難易度が高くなります。 ヒットチェックが厳し過ぎる場合、ユーザーはプレイすることに苦痛を感じ、そのゲームを投げ出してしまうかもしれません。 またスマートフォンの普及に伴い画面上の物体を指で直接動かすアプリが増えましたが、そのようなタイプのゲームではヒットチェックが操作性の良し悪しに影響します。 つまりヒットチェックは単なる数値比較ではなく、ゲームの面白さに直結する重要な要素であるのです。

ヒットチェックにはいくつかの方法がありますが、 最も基本となる矩形によるヒットチェックと円によるヒットチェックの２つを解説します。 また将来３Ｄゲームを制作したい方のために、３Ｄのヒットチェックも概要を説明します。

(1)矩形によるヒットチェック

２つの物体を矩形（長方形）として判定を行う方法です。 次のような２つキャラクターの表示位置（XY座標）と画像の幅と高さを用い、接触しているか調べてみましょう。

主人公キャラ( x, y )、幅w、高さh　→　中心座標は( x+w/2, y+h/2 )
敵キャラ( X, Y )、幅W、高さH　→　中心座標は( X+W/2, Y+H/2 )
中心間のX方向の距離dxは (x+w/2) - (X+W/2) の絶対値
中心間のY方向の距離dyは (y+h/2) - (Y+H/2) の絶対値
dx < (w/2+W/2) かつ dy < (h/2+H/2) であれば２つの矩形は重なっています。

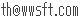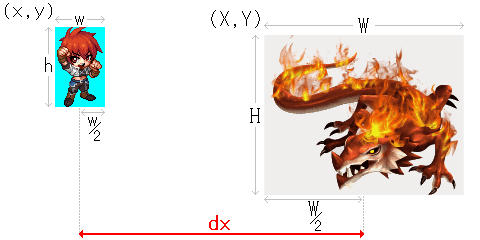
絶対値を求める命令 Math.abs
(x+w/2) - (X+W/2) と (y+h/2) - (Y+H/2) は位置関係により、値がプラスになったりマイナスになったりしますので、 Math.abs命令を使って、それぞれの絶対値で調べます。


実際の判定を行うサンプルを見てみましょう。
２つの矩形をタップ（マウスではドラッグドロップ）で動かすことができます。
example221.html　←　動作の確認
ソースコードは次のようになります。
01<!DOCTYPE html>
02<html lang="ja">
03<head>
04<meta charset="utf-8">
05<meta name="viewport" content="width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0 user-scalable=no">
06<title>JavaScriptのテストプログラム</title>
07</head>
08<body>
09<canvas style="position:absolute; top:0; bottom:0; left:0; right:0; margin:auto;" id="bg"></canvas>
10<script>
11var winW = window.innerWidth;
12var winH = window.innerHeight;
13var canvas = document.getElementById("bg");
14canvas.width = winW;
15canvas.height = winH;
16var cnt = canvas.getContext("2d");
17cnt.font = "32px monospace";
18cnt.textAlign = "center";
19
20var SCALE = winW / 800;
21cnt.scale( SCALE, SCALE );
22
23//マウスとタップの判定
24var tapX = 0, tapY = 0, tapC = 0;
25
26if( 'ontouchend' in document ) {
27 canvas.addEventListener( "touchstart", touchStart );
28 canvas.addEventListener( "touchmove", touchMove );
29 canvas.addEventListener( "touchend", touchEnd );
30 function touchStart(event) {
31  event.preventDefault();
32  var rect = event.target.getBoundingClientRect();
33  tapX = event.touches[0].clientX-rect.left;
34  tapY = event.touches[0].clientY-rect.top;
35  transformXY();
36  tapC = 1;
37 }
38 function touchMove(event) {
39  event.preventDefault();
40  var rect = event.target.getBoundingClientRect();
41  tapX = event.touches[0].clientX-rect.left;
42  tapY = event.touches[0].clientY-rect.top;
43  transformXY();
44 }
45 function touchEnd(event) {
46  event.preventDefault();
47  tapC = 0;
48 }
49}
50else {
51 canvas.addEventListener( "mousedown", mouseDown );
52 canvas.addEventListener( "mousemove", mouseMove );
53 canvas.addEventListener( "mouseup", mouseUp );
54 function mouseDown(event) {
55  var rect = event.target.getBoundingClientRect();
56  tapX = event.clientX-rect.left;
57  tapY = event.clientY-rect.top;
58  transformXY();
59  tapC = 1;
60 }
61 function mouseMove(event) {
62  var rect = event.target.getBoundingClientRect();
63  tapX = event.clientX-rect.left;
64  tapY = event.clientY-rect.top;
65  transformXY();
66 }
67 function mouseUp(event) {
68  tapC = 0;
69 }
70}
71
72function transformXY() {
73 tapX = toInt(tapX/SCALE);
74 tapY = toInt(tapY/SCALE);
75}
76
77function toInt( val ) {
78 return parseInt(val);
79}
80
81//描画用の関数
82function fText( str, x, y, col ) {//文字表示
83 cnt.fillStyle = col;
84 cnt.fillText( str, x, y );
85}
86
87function fRect( x, y, w, h, col ) {//矩形
88 cnt.fillStyle = col;
89 cnt.fillRect( x, y, w, h );
90}
91
92//ヒットチェックを行う関数
93function hitCheck( x1, y1, w1, h1, x2, y2, w2, h2 ) {
94 var dx = Math.abs( (x1+w1/2) - (x2+w2/2) );
95 var dy = Math.abs( (y1+h1/2) - (y2+h2/2) );
96 if( dx < w1/2+w2/2 && dy < h1/2+h2/2 ) return true;
97 return false;
98}
99
100var x = 100, y = 100, w = 160, h = 240;
101var X = 400, Y = 200, W = 360, H = 280;
102
103window.onload = mainProc();
104function mainProc() {
105 fRect( 0, 0, 800, 1200, "#000" );
106
107 if( tapC == 1 ) {
108  if( x < tapX && tapX < x+w && y < tapY && tapY < y+h ) {
109  x = tapX-w/2;
110  y = tapY-h/2;
111  }
112  else if( X < tapX && tapX < X+W && Y < tapY && tapY < Y+H ) {
113  X = tapX-W/2;
114  Y = tapY-H/2;
115  }
116 }
117
118 fRect( x, y, w, h, "#00f" );
119 fRect( X, Y, W, H, "#f00" );
120
121 if( hitCheck( x, y, w, h, X, Y, W, H ) == true ) fText( "２つの矩形は重なっている", 400, 200, "#ff0" );
122
123 setTimeout( mainProc, 50 );
124}
125</script>
126</body>
127</html>

ヒットチェックを行っているのが次の関数で、２つの矩形が重なっているならtrue、重なっていないならfalseを返します。

function hitCheck( x1, y1, w1, h1, x2, y2, w2, h2 ) {
 var dx = Math.abs( (x1+w1/2) - (x2+w2/2) );
 var dy = Math.abs( (y1+h1/2) - (y2+h2/2) );
 if( dx < w1/2+w2/2 && dy < h1/2+h2/2 ) return true;
 return false;
}



ソースコードのポイントの復習（①～③）と、新たに加えたポイントを説明します。

①画面の拡大縮小を防ぐmeta要素

<meta name="viewport" content="width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0 user-scalable=no">


②キャンバスをブラウザ中央に配置するスタイル属性

<canvas style="position:absolute; top:0; bottom:0; left:0; right:0; margin:auto;" id="bg"></canvas>


③キャンバスをブラウザ内いっぱいに広げるJavaScriptのコード

var winW = window.innerWidth;
var winH = window.innerHeight;
及び
canvas.width = winW;
canvas.height = winH;


新たに加えたポイントは２つあり、１つ目は機種を問わず全てのデバイスで描画に使う画面（キャンバス）の仮想サイズを一定にする方法です。 今回は横幅800ドットの仮想サイズにしています。

【ポイント１】　画面の仮想サイズを設定する

var SCALE = winW / 800;
cnt.scale( SCALE, SCALE );

scale命令はキャンバスに図形や画像を表示する際のx方向及びy方向の伸縮率を設定します。 上記の記述により、例えばwinWが1600ドットの端末ではSCALE=2.0となり、この値がセットされ図形は２倍の大きさで描画されます。 winWが400ドットではSCALE=0.5となり、図形は１／２サイズで描画されます。 これで画面のドット数を問わず、全てのデバイスで同じ比率でグラフィックが表示されます。

※横幅に対応する比率を設定していますので、次の図のように横幅に対して同じ比率となります
これを行わず、例えば横480ドットのスマートフォンで幅400ドットの四角を描くと画面を埋めるような大きな四角になりますが、 横1920ドットのタブレットでは小さな四角となります。

スケール率を設定してもタッチやマウス判定で取得する座標は実座標のままとなります。 そこで次のような関数を用意し、タッチやマウスの位置を仮想サイズ上の座標値に変換しています。

【ポイント２】　座標値を変換する

function transformXY() {
 tapX = toInt(tapX/SCALE);
 tapY = toInt(tapY/SCALE);
}

toInt()は値を整数にする関数で、これもソース内で定義しています。

Math.floor と parseInt
プログラミングでは数値の少数点以下を切り捨て整数にして使うことがあります。 少数点以下を切る命令には Math.floor(値) と parseInt(値) があります。 Math.floorは1-3(3)で説明したようにマイナスの値の時に注意が必要です。 parseIntはプラスの値でもマイナスの値でも小数点以下を切り捨てます。 今回のソースコードのtoInt関数にはparseIntを用いています。
※厳密にはMath.floorは数値を扱い、parseIntは数値と文字列を扱うことができ、 これら２つの命令は挙動の詳細は違うのですが、parseIntは少数部分を切り捨てる命令と考えて問題ございません。



さて、今回の方法は矩形同士であれば正確にヒットチェックできます。 しかしながらゲームのキャラクターは全て四角というわけではなく、色々な形状になっています。 次の絵のような場合、左側のヒットチェックは的確ですが、 右側のように矩形は重なっているがキャラクターの絵は重ならないことがあり、 この状態で接触したと判定すると、ユーザーは接触していないのに接触したことにされたわけですので、納得できません。



このような場合はヒットチェックを行う値を次のようにします。

if( dx < w1/2+w2/2 && dy < h1/2+h2/2 ) return true;
　↓
if( dx < (w1/2+w2/2)*0.9 && dy < (h1/2+h2/2)*0.9 ) return true;

(w/2+W/2)*0.9 と dy < (h/2+H/2)*0.9 というように画像の幅と高さより小さな値で判定すれば、キャラクター同士がしっかり重なった時に接触したことになります。 掛ける小数の値が小さいほど接触判定が甘くなるわけです。

少数を掛けるのは簡易的に判定を調整する方法です。 ヒットチェックを甘くし過ぎると、アクションゲームであれば敵に接触したのにダメージを受けなかったとユーザーが感じる可能性が出てきます。 キャラクターの形状によっては次に解説する円によるヒットチェックが適しています。

(2)円によるヒットチェック

キャラクターを円に見立て２物体間の距離で判定する方法です。 次の図で緑色の線が２つのキャラクターの中心間の距離です。 この距離が r + R より小さければ２つの物体（円）は重なっていることになります。

高校数学で学ぶ、(x1,y1) と (x2,y2) の２点間の距離の式は次のようになります。

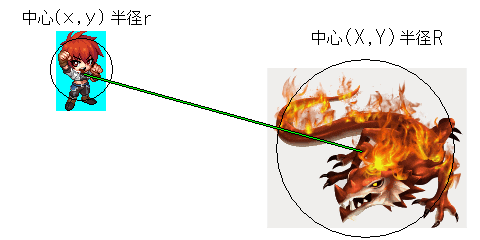
√(x1-x2)^2 + (y1-y2)^2


平方根を求めるJavaScriptの命令は Math.sqrt() です。
ｎ乗を書き表すのに使う ^ の記号は、JavaScriptでは別の意味（ビット演算子）になりますので、 上図のキャラクターの距離は次のように記述します。

Math.sqrt( (x-X)*(x-X) + (y-Y)*(y-Y) );

もしくはｎ乗を求める命令Math.pow( 底数, 指数 )を用い、

Math.sqrt( Math.pow(x-X,2) + Math.pow(y-Y,2) );


ビット演算子
プログラミングの世界にはビット演算子といわれるものがあります。

・ビットをシフトする << 、 >>
・AND（論理積）を求める &
・OR（論理和）を求める |
・XOR（排他的論理和）を求める ^
・１との補数を求める ~

ビット演算子の説明は、現時点では本講座の目指すところ（みなさんがゲームを作れるようになるという目標）を超えた範囲ですので、割愛しますが、 プロのゲームプログラマーを目指す方にとってはビット演算子の知識も必要となりますので、そのような方はぜひネットで調べてみて下さい。


距離による判定のサンプルを見てみましょう。
example222.html　←　動作の確認
ソースコードは次のようになります。
※01～80行は(1)と一緒ですので省略します。
81//描画用の関数
82function fText( str, x, y, col ) {//文字表示
83 cnt.fillStyle = col;
84 cnt.fillText( str, x, y );
85}
86
87function fRect( x, y, w, h, col ) {//矩形
88 cnt.fillStyle = col;
89 cnt.fillRect( x, y, w, h );
90}
91
92function fArc( x, y, r, col ) {//円
93 cnt.fillStyle = col;
94 cnt.beginPath();
95 cnt.arc( x, y, r, 0, Math.PI*2, false );
96 cnt.fill();
97 cnt.restore();
98}
99
100//ヒットチェックを行う関数
101function hitCheck2( x1, y1, r1, x2, y2, r2 ) {
102 var dis = Math.sqrt( (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) );
103 if( dis < r1+r2 ) return true;
104 return false;
105}
106
107var x = 200, y = 200, r = 120;
108var X = 600, Y = 300, R = 180;
109
110window.onload = mainProc();
111function mainProc() {
112 fRect( 0, 0, 800, 1200, "#000" );
113
114 if( tapC == 1 ) {
115  if( x-r < tapX && tapX < x+r && y-r < tapY && tapY < y+r ) {
116  x = tapX;
117  y = tapY;
118  }
119  else if( X-R < tapX && tapX < X+R && Y-R < tapY && tapY < Y+R ) {
120  X = tapX;
121  Y = tapY;
122  }
123 }
124
125 fArc( x, y, r, "#0f0" );
126 fArc( X, Y, R, "#a0f" );
127
128 if( hitCheck2( x, y, r, X, Y, R ) == true ) fText( "２つの円は重なっている", 400, 200, "#ff0" );
129
130 setTimeout( mainProc, 50 );
131}
132</script>
133</body>
134</html>

ヒットチェックを行っているのが次の関数です。

function hitCheck2( x1, y1, r1, x2, y2, r2 ) {
 var dis = Math.sqrt( (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) );
 if( dis < r1+r2 ) return true;
 return false;
}

矩形による判定と同様に、重なっているならtrue、重なっていないならfalseを返します。

◇コラム◇　ヒットチェックは甘めで行きましょう
無料のアプリが大量に配信される現在では、ユーザーが遊ぶゲームはいくらでもあります。 これはクリアできないと感じるゲームはすぐに削除されるのが現実です。 ですので今のゲームは甘いくらいがちょうど良いでしょう。 多くのユーザーが先まで遊べるやさしめの難易度が良いというわけです。


(3)３Ｄゲームのヒットチェック

３Ｄのゲームはキャラクターや背景のモデルデータを用意し表示しています。 ３Ｄゲームの開発環境の多くには、２つのモデルデータが接触しているか判定する命令が用意されています。 そういった命令を使えばてっとり早く三次元でのヒットチェックができますが、自分で作ったソースコードで判定することを考えてみましょう。

(1)と(2)で説明したヒットチェックは２次元の判定であり、位置、幅と高さ（あるいは半径）という二次元の値（ＸＹの値）で判定しています。 三次元のヒットチェックも、ここで解説した方法の延長線上の考え方で行うことができます。 ３Ｄゲーム＝三次元の世界は、高さのＺ軸を含めた三次元の値（ＸＹＺの値）で判定します。具体的には、
①物体を直方体に見立て、２つの直方体が重なるかで判定（二次元では矩形の判定に相当する）
②物体を球体に見立て、中心間の距離で判定（二次元では円の判定に相当する）
となります。

例として中心間の距離で判定する場合、半径r1の球の中心が空間座標(x1,y1,z1)にあり、半径r2の球の中心が(x2,y2,z2)にあるなら、 ２つの球の中心間の距離は √(x1-x2)^2 + (y1-y2)^2+ (z1-z2)^2 であり、 この値が (r1+r2) より小さければ接触していることになります。

◇コラム◇　プログラマーを目指す中高生へ、今回は真面目な話です
ゲームの開発環境によっては便利な命令が用意されており、ここで触れたように、命令の使い方さえ覚えれば理屈を知らなくとも、三次元のヒットチェックもできるようになっています。 例えばUnityというツールは使い方を学べば、どなたでも高度なゲームを完成させることができます。 学校であるいは独学でUnityを学び、ゲーム会社の募集にUnityで作ったゲームを送り、面接に進めたとします。 企業はプログラマーとして本当に使える人材であるか試すために技術的な質問をします。 プログラミングの根底にある技術を知らないと、正しい受け答えは難しく、残念ながら不採用となってしまうでしょう。 その技術とはずばり“数学”と“物理”です。 また世の中に普及しているプログラミング言語は“英語”です。 コンピューターの最新の技術情報はまず英語のサイトに掲載されることが多く、 プログラマーは英語で書かれた情報を調べることもあります。 プログラマーを目指す諸君は理系の教科と英語を頑張って下さい。 ・・・と難しいことを書きましたが、趣味のゲーム制作ではそこまでシビアに考える必要はございません。 本講座はプログラミング初心者の方に理解して頂ける内容で連載を続けて参ります。


前のページへ　／　次のページへ
お気軽にお問い合わせ下さい →